Ions in nanoconfinement

This application studies ionic structure in electrolyte solutions in nanochannels with planar uncharged surfaces and can use multiple molecular dynamics (MD) codes including LAMMPS which run on HPC supercomputers with OpenMP and MPI parallelization.

Metadata

Model nanoconfinement.json

Datasets nanoconfinement.json

This application 1 2 3 studies ionic structure in electrolyte solutions in nanochannels with planar uncharged surfaces and can use multiple molecular dynamics (MD) codes including LAMMPS 4 which run on HPC supercomputers with OpenMP and MPI parallelization.

A dense neural-net (NN) was used to learn 150 final state characteristics based on the input of 5 parameters with typical results shown in fig. 2(b) with the NN results for three important densities tracking well the MD simulation results for a wide range of unseen input system parameters. Fig. 3(a,b) shows two typical density profiles with again the NN prediction tracking well the simulation. Input quantities were confinement length, positive ion valency, negative ion valency, salt concentration, and ion diameter. Figure 2(a) shows the runtime architecture for dynamic use and update of the NN and our middleware discussed in Sec. 3.2.6 will generalize this. The inference time for this on a single core is 104 times faster than the parallel code which is itself 100 times the sequential code. This surrogate approach is the first-of-its-kind in the area of simulating charged soft-matter systems and there are many other published papers in both biomolecular and material science presenting similar successful surrogates 5 with a NN architecture similar to fig. 3(c).

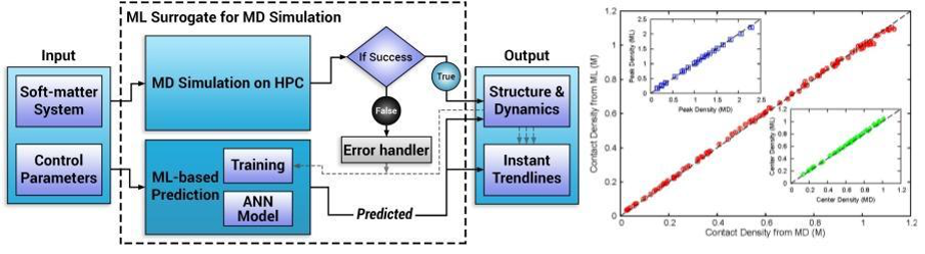
Fig. 2 a) Architecture of dynamic training of ML surrogate and b) Comparison of three final state densities (peak, contact, and center) between MD simulations and NN surrogate predictions [^5] [^51].

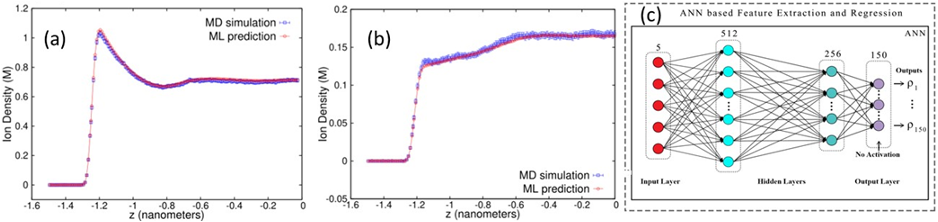
Fig. 3 (a,b) Two density profiles of confined ions for very different input parameters and comparing MD and NN. (c) Fully connected deep learning network used to learn the final densities. ReLU activation units are in the 512 and 256 node hidden layers. The output values were learned on 150 nodes.

References

  1. JCS Kadupitiya , Geoffrey C. Fox , and Vikram Jadhao, “Machine learning for performance enhancement of molecular dynamics simulations,” in International Conference on Computational Science ICCS2019, Faro, Algarve, Portugal, 2019 [Online]. Available: http://dsc.soic.indiana.edu/publications/ICCS8.pdf ↩︎

  2. J. C. S. Kadupitiya, F. Sun, G. Fox, and V. Jadhao, “Machine learning surrogates for molecular dynamics simulations of soft materials,” J. Comput. Sci., vol. 42, p. 101107, Apr. 2020 [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1877750319310609 ↩︎

  3. “Molecular Dynamics for Nanoconfinement.” [Online]. Available: https://github.com/softmaterialslab/nanoconfinement-md. [Accessed: 11-May-2020] ↩︎

  4. S. Plimpton, “Fast Parallel Algorithms for Short Range Molecular Dynamics,” J. Comput. Phys., vol. 117, pp. 1–19, 1995 [Online]. Available: http://faculty.chas.uni.edu/~rothm/Modeling/Parallel/Plimpton.pdf ↩︎

  5. Geoffrey Fox, Shantenu Jha, “Learning Everywhere: A Taxonomy for the Integration of Machine Learning and Simulations,” in IEEE eScience 2019 Conference, San Diego, California [Online]. Available: https://arxiv.org/abs/1909.13340 ↩︎

Last modified January 26, 2024: Fixed typos (a1d6fc4)