This is the multi-page printable view of this section. Click here to print.

Return to the regular view of this page.

Surrogates

A list of surrogates we look at

A list of surrogates

1 - AutoPhaseNN: unsupervised physics-aware deep learning of 3D nanoscale Bragg coherent diffraction imaging

A DL-based approach which learns to solve the phase problem in 3D X-ray Bragg coherent diffraction imaging (BCDI) without labeled data.

Metadata

Model autophasenn.json

Datasets autoPhaseNN_aicdi.json

Adapted from Yao, Y. et. al 1 under CC-BY 2

AutoPhaseNN 1, a physics-aware unsupervised deep convolutional neural network (CNN) that learns to solve the phase problem without ever being shown real space images of the sample amplitude or phase. By incorporating the physics of the X-ray scattering into the network design and training, AutoPhaseNN learns to predict both the amplitude and phase of the sample given the measured diffraction intensity alone. Additionally, unlike previous deep learning models, AutoPhaseNN does not need the ground truth images of sample’s amplitude and phase at any point, either in training or in deployment. Once trained, the physical model is discarded and only the CNN portion is needed which has learned the data inversion from reciprocal space to real space and is ~100 times faster than the iterative phase retrieval with comparable image quality. Furthermore, we show that by using AutoPhaseNN’s prediction as the learned prior to iterative phase retrieval, we can achieve consistently higher image quality, than neural network prediction alone, at 10 times faster speed than iterative phase retrieval alone.

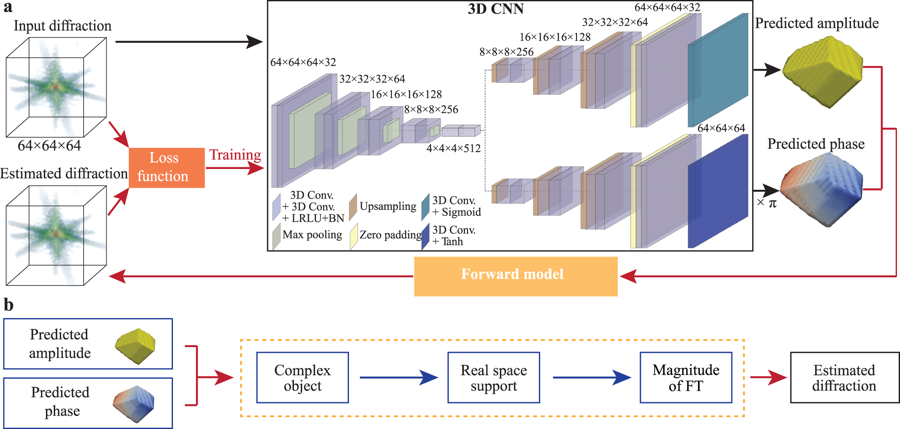
Fig. 1: Schematic of the neural network structure of AutoPhaseNN model during training. a) The model consists of a 3D CNN and the X-ray scattering forward model. The 3D CNN is implemented with a convolutional auto-encoder and two deconvolutional decoders using the convolutional, maximum pooling, upsampling and zero padding layers. The physical knowledge is enforced via the Sigmoid and Tanh activation functions in the final layers. b The X-ray scattering forward model includes the numerical modeling of diffraction and the image shape constraints. It takes the amplitude and phase from the 3D CNN output to form the complex image. Then the estimated diffraction pattern is obtained from the FT of the current estimation of the real space image.
Image from: Yao, Y. et al / CC-BY

References

  1. Yao, Y., Chan, H., Sankaranarayanan, S. et al. AutoPhaseNN: unsupervised physics-aware deep learning of 3D nanoscale Bragg coherent diffraction imaging. npj Comput Mater 8, 124 (2022). https://doi.org/10.1038/s41524-022-00803-w ↩︎ ↩︎

  2. http://creativecommons.org/licenses/by/4.0/ ↩︎

2 - Calorimeter surrogates

The Kaggle calorimeter challenge uses generative AI to produce a surrogate for the Monte Carlo calculation of a calorimeter response to an incident particle (ATLAS data at LHC calculated with GEANT4).

Overview

The Kaggle calorimeter challenge uses generative AI to produce a surrogate for the Monte Carlo calculation of a calorimeter response to an incident particle (ATLAS data at LHC calculated with GEANT4). Variational Auto Encoders, GANs, Normalizing Flows, and Diffusion Models. We also have a surrogate using a Quantum Computer (DWAVE) annealer to generate random samples. We have identified four different surrogates that are available openly from Kaggle and later submissions.

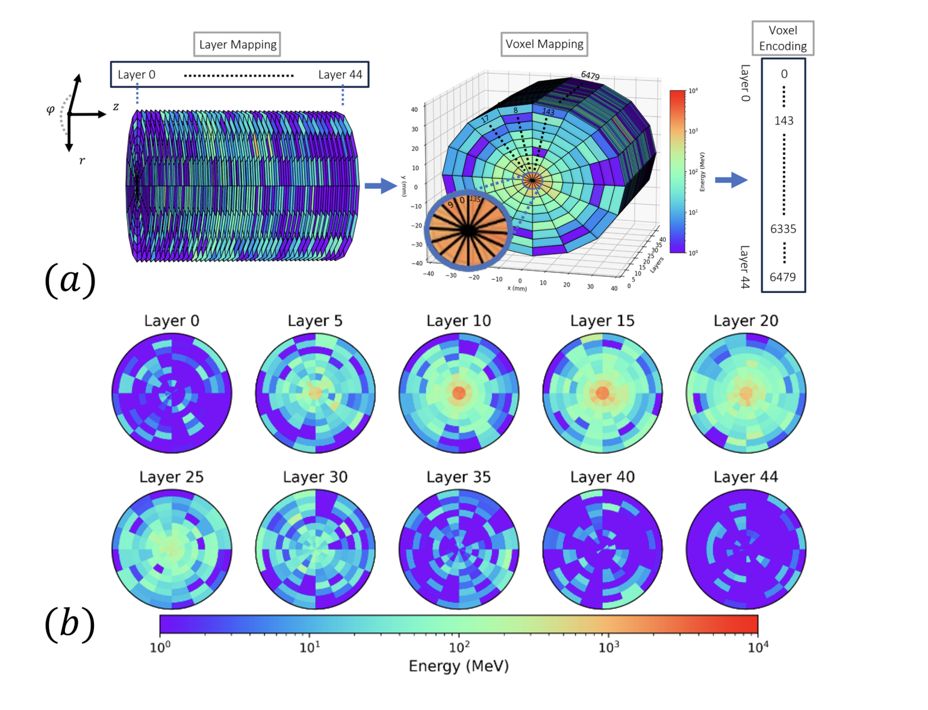
Figure 1: CaloChallenge Dataset.

Details

Accurate simulation plays a crucial role in particle physics by bridging theoretical models with experimental data to uncover the universe’s fundamental properties. At the Large Hadron Collider (LHC), simulations based on Monte Carlo methods model the interactions of billions of particles, including complex calorimeter shower events—cascades of secondary particles produced when high-energy particles hit detector materials. The widely-used Geant4 1 simulation toolkit provides highly detailed physics-based simulations, but its computational cost is extremely high, making up over 75% of the total simulation time 2. With the upcoming High-Luminosity LHC (HL-LHC) 3,4 upgrade in 2029, the collider will generate larger datasets with higher precision requirements, significantly increasing the demand for computational resources. To mitigate this, researchers are exploring generative models commonly used in image and text generation—as surrogate models that can generate realistic calorimeter showers at a fraction of the computational cost. In recent years, several approaches based on Generative Adversarial Networks(GAN) 5, 6, 7, 8, 9, 10, Diffusion 11 12, 13, 14, 15, 16, 17, 18, 19, Variational Autoencoders (VAEs) 20, 21, 22, 23, 24, 25, 26, 27, 28 and Normalizing Flows 29, 30, 31, 32, 33, 34, 35 have been proposed. However, evaluating these models remains challenging because the physical characteristics of calorimeter showers differ significantly from traditional image- and text-based data. 36, 37 conducted a rigorous evaluation of these generative models using standard datasets and a diverse set of metrics derived from physics, computer vision, and statistics. Although 36 sheds light on the existent correlations between layers, they do not quantify correlations between layers and voxels. In this work, we propose Correlation Frobenius Distance (CFD), an evaluation metric for generative models of calorimeter shower simulation. This metric measures how the consecutive layers and voxels of generated samples are correlated with each other compared to Geant4 samples. CFD helps evaluate the consistency of energy deposition patterns across layers, capturing the spatial correlations in the calorimeter shower. Lower CFD values indicate that the generated samples better preserve the correlations observed in Geant4 simulations. We compared four different models (CaloDream 19, CaloScore v2 18, CaloDiffusion 27, and CaloINN 33) on Dataset 2 38 from CaloChallenge 2022 13 for CFD, our observation reveals that CaloDream can capture correlations between consecutive layers and voxels the best. Furthermore, we explored the impact of using full versus mixed precision modes during inference for CaloDiffusion. Our observation shows that mixed precision inference does not speed up inference for Dataset 1 39 and Dataset 2 39.​ However, it significantly improves inference time for Dataset 3 39, without compromising performance.​ The Code is available in GitHub at 40.

Additional relevant references include:

41, 42,

Team contributed refernces include

43, 44, 45, 46,

References

Team contributed refernces are marked in bold

  1. Agostinelli, Sea, et al. “GEANT4—a simulation toolkit.” Nuclear instruments and methods in physics research section A: Accelerators, Spectrometers, Detectors and Associated Equipment 506.3 (2003): 250-303. ↩︎

  2. Muškinja, Miha, John Derek Chapman, and Heather Gray. “Geant4 performance optimization in the ATLAS experiment.” EPJ Web of Conferences. Vol. 245. EDP Sciences, 2020. ↩︎

  3. “New Schedule for CERN’s Accelerators.” CERN, 5 Dec. 2023, [https://home.cern/news/news/accelerators/new-schedule-cerns-accelerators]:(https://home.cern/news/news/accelerators/new-schedule-cerns-accelerators). Accessed 28 Feb. 2025. ↩︎

  4. “Computing at CERN.” CERN, https://home.web.cern.ch/science/computing. Accessed 28 Feb. 2025. ↩︎

  5. ATLAS collaboration. “Fast simulation of the ATLAS calorimeter system with Generative Adversarial Networks.” ATLAS PUB Note, CERN, Geneva (2020). ↩︎

  6. Ghosh, Aishik, and ATLAS collaboration. “Deep generative models for fast shower simulation in ATLAS.” Journal of Physics: Conference Series. Vol. 1525. No. 1. IOP Publishing, 2020. ↩︎

  7. Giannelli, Michele Faucci, and Rui Zhang. “CaloShowerGAN, a generative adversarial network model for fast calorimeter shower simulation.” The European Physical Journal Plus 139.7 (2024): 597. ↩︎

  8. Paganini, Michela, Luke de Oliveira, and Benjamin Nachman. “Accelerating science with generative adversarial networks: an application to 3D particle showers in multilayer calorimeters.” Physical review letters 120.4 (2018): 042003. ↩︎

  9. de Oliveira, Luke, Michela Paganini, and Benjamin Nachman. “Learning particle physics by example: location-aware generative adversarial networks for physics synthesis.” Computing and Software for Big Science 1.1 (2017): 4. ↩︎

  10. Paganini, Michela, Luke de Oliveira, and Benjamin Nachman. “CaloGAN: Simulating 3D high energy particle showers in multilayer electromagnetic calorimeters with generative adversarial networks.” Physical Review D 97.1 (2018): 014021. ↩︎

  11. Acosta, Fernando Torales, et al. “Comparison of point cloud and image-based models for calorimeter fast simulation.” Journal of Instrumentation 19.05 (2024): P05003. ↩︎

  12. Amram, Oz, and Kevin Pedro. “Denoising diffusion models with geometry adaptation for high fidelity calorimeter simulation.” Physical Review D 108.7 (2023): 072014. ↩︎

  13. Buhmann, Erik, et al. “CaloClouds: fast geometry-independent highly-granular calorimeter simulation.” Journal of Instrumentation 18.11 (2023): P11025. ↩︎ ↩︎

  14. Buhmann, Erik, et al. “CaloClouds II: ultra-fast geometry-independent highly-granular calorimeter simulation.” Journal of Instrumentation 19.04 (2024): P04020. ↩︎

  15. Cresswell, Jesse C., and Taewoo Kim. “Scaling Up Diffusion and Flow-based XGBoost Models.” arXiv preprint arXiv:2408.16046 (2024). ↩︎

  16. Madula, T., and V. M. Mikuni. “CaloLatent: Score-based Generative Modelling in the Latent Space for Calorimeter Shower Generation NeurIPS Workshop on Machine Learning and the Physical Sciences URL https://ml4physicalsciences. github. io/2023/files.” NeurIPS_ ML4PS_2023_19. pdf (2023). ↩︎

  17. Mikuni, Vinicius, and Benjamin Nachman. “Score-based generative models for calorimeter shower simulation.” Physical Review D 106.9 (2022): 092009. ↩︎

  18. Mikuni, Vinicius, and Benjamin Nachman. “CaloScore v2: single-shot calorimeter shower simulation with diffusion models.” Journal of Instrumentation 19.02 (2024): P02001. ↩︎ ↩︎

  19. Favaro, Luigi, et al. “CaloDREAM–Detector Response Emulation via Attentive flow Matching.” arXiv preprint arXiv:2405.09629 (2024). ↩︎ ↩︎

  20. Cresswell, Jesse C., et al. “CaloMan: Fast generation of calorimeter showers with density estimation on learned manifolds.” arXiv preprint arXiv:2211.15380 (2022). ↩︎

  21. Buhmann, Erik, et al. “Decoding photons: Physics in the latent space of a BIB-AE generative network.” EPJ Web of Conferences. Vol. 251. EDP Sciences, 2021. ↩︎

  22. Buhmann, Erik, et al. “Getting high: High fidelity simulation of high granularity calorimeters with high speed.” Computing and Software for Big Science 5.1 (2021): 13. ↩︎

  23. Diefenbacher, Sascha, et al. “New angles on fast calorimeter shower simulation.” Machine Learning: Science and Technology 4.3 (2023): 035044. ↩︎

  24. Salamani, Dalila, Anna Zaborowska, and Witold Pokorski. “MetaHEP: Meta learning for fast shower simulation of high energy physics experiments.” Physics Letters B 844 (2023): 138079. ↩︎

  25. Abhishek, Abhishek, et al. “CaloDVAE: Discrete variational autoencoders for fast calorimeter shower simulation.” arXiv preprint arXiv:2210.07430 (2022). ↩︎

  26. Caloqvae: Simulating high-energy particle calorimeter interactions using hybrid quantum-classical generative models ↩︎

  27. Hoque, Sehmimul, et al. “CaloQVAE: Simulating high-energy particle-calorimeter interactions using hybrid quantum-classical generative models.” The European Physical Journal C 84.12 (2024): 1-7. ↩︎ ↩︎

  28. Lu, Ian, et al. “Zephyr quantum-assisted hierarchical Calo4pQVAE for particle-calorimeter interactions.” arXiv preprint arXiv:2412.04677 (2024). ↩︎

  29. Krause, Claudius, and David Shih. “Fast and accurate simulations of calorimeter showers with normalizing flows.” Physical Review D 107.11 (2023): 113003. ↩︎

  30. Krause, Claudius, Ian Pang, and David Shih. “CaloFlow for CaloChallenge dataset 1.” SciPost Physics 16.5 (2024): 126. ↩︎

  31. Buckley, Matthew R., et al. “Inductive simulation of calorimeter showers with normalizing flows.” Physical Review D 109.3 (2024): 033006. ↩︎

  32. Diefenbacher, S., et al. “L2LFlows: generating high-fidelity 3D calorimeter images (2023).” arXiv preprint arXiv:2302.11594 18: P10017. ↩︎

  33. Ernst, Florian, et al. “Normalizing flows for high-dimensional detector simulations.” arXiv preprint arXiv:2312.09290 (2023). ↩︎ ↩︎

  34. Liu, Junze, et al. “Geometry-aware autoregressive models for calorimeter shower simulations.” arXiv preprint arXiv:2212.08233 (2022). ↩︎

  35. Schnake, Simon, Dirk Krücker, and Kerstin Borras. “CaloPointFlow II generating calorimeter showers as point clouds.” arXiv preprint arXiv:2403.15782 (2024). ↩︎

  36. Ahmad, Farzana Yasmin, Vanamala Venkataswamy, and Geoffrey Fox. “A comprehensive evaluation of generative models in calorimeter shower simulation.” arXiv preprint arXiv:2406.12898 (2024). ↩︎ ↩︎

  37. Krause, Claudius, et al. “Calochallenge 2022: A community challenge for fast calorimeter simulation.” arXiv preprint arXiv:2410.21611 (2024). ↩︎

  38. Ahmad, F. Y. Generated Samples of Dataset 2 from Calochallenge_2022. Zenodo, 17 Feb. 2025, doi:10.5281/zenodo.14883798. ↩︎

  39. CaloChallenge Homepage*, calochallenge.github.io/homepage/. Accessed 3 Mar. 2025. ↩︎ ↩︎ ↩︎

  40. GitHub: https://github.com/Aaheer17/Benchmarking_Calorimeter_Shower_Simulation_Generative_AI/tree/main ↩︎

  41. Michele Faucci Giannelli, Gregor Kasieczka, Claudius Krause, Ben Nachman, Dalila Salamani, David Shih, Anna Zaborowska, Fast calorimeter simulation challenge 2022 - dataset 1,2 and 3 [data set]. zenodo., https://doi.org/10.5281/zenodo.8099322, https://doi.org/10.5281/zenodo.6366271, https://doi.org/10.5281/zenodo.6366324 (2022). ↩︎ ↩︎

  42. ATLAS Collaboration, ATLAS software and computing HL-LHC roadmap, Tech. Rep. (Technical report, CERN, Geneva. http://cds.cern.ch/record/2802918, 2022). ↩︎ ↩︎ ↩︎

  43. Conditioned quantum-assisted deep generative surrogate for particle-calorimeter interactions, J Quetzalcoatl Toledo-Marin, Sebastian Gonzalez, Hao Jia, Ian Lu, Deniz Sogutlu, Abhishek Abhishek, Colin Gay, Eric Paquet, Roger Melko, Geoffrey C Fox, Maximilian Swiatlowski, Wojciech Fedorko, 2024/10/30 arXiv preprint arXiv:2410.22870, Abstract: Particle collisions at accelerators such as the Large Hadron Collider, recorded and analyzed by experiments such as ATLAS and CMS, enable exquisite measurements of the Standard Model and searches for new phenomena. Simulations of collision events at these detectors have played a pivotal role in shaping the design of future experiments and analyzing ongoing ones. However, the quest for accuracy in Large Hadron Collider (LHC) collisions comes at an imposing computational cost, with projections estimating the need for millions of CPU-years annually during the High Luminosity LHC (HL-LHC) run 42. Simulating a single LHC event with Geant4 currently devours around 1000 CPU seconds, with simulations of the calorimeter subdetectors in particular imposing substantial computational demands 42. To address this challenge, we propose a conditioned quantum-assisted deep generative model. Our model integrates a conditioned variational autoencoder (VAE) on the exterior with a conditioned Restricted Boltzmann Machine (RBM) in the latent space, providing enhanced expressiveness compared to conventional VAEs. The RBM nodes and connections are meticulously engineered to enable the use of qubits and couplers on D-Wave’s Pegasus-structured \textit{Advantage} quantum annealer (QA) for sampling. We introduce a novel method for conditioning the quantum-assisted RBM using flux biases. We further propose a novel adaptive mapping to estimate the effective inverse temperature in quantum annealers. The effectiveness of our framework is illustrated using Dataset 2 of the CaloChallenge 41. ↩︎

  44. Calorimeter Surrogate Research, Geoffrey Fox University of Virginia, 2024 https://docs.google.com/document/d/19g0Avj9SYbVH7qSxoVUnnFKeGMuBdD9JCHVmBQB466M/ ↩︎

  45. Poster: https://drive.google.com/file/d/1PUiNDju_8N_wsDKI_W-g-jyCHb_5Hepo/ ↩︎

  46. Extended abstract: Correlation Frobenius Distance: A Metric for Evaluating Generative Models in Calorimeter Shower Simulation, Farzana Yasmin Ahmada, Vanamala Venkataswamya, Geoffrey Fox, University of Virginia, https://docs.google.com/document/d/1ndHkJY41_pHYZZne58B4_7HJQKTCxPzeMWVMJ0bsnOE ↩︎

3 - Virtual tissue

This surrugate simulates a virtual tissue

Overview

Neural networks (NNs) have been demonstrated to be a viable alternative to traditional direct numerical evaluation algorithms, with the potential to accelerate computational time by several orders of magnitude. In the present paper we study the use of encoder-decoder convolutional neural network (CNN) algorithms as surrogates for steady-state diffusion solvers. The construction of such surrogates requires the selection of an appropriate task, network architecture, training set structure and size, loss function, and training algorithm hyperparameters. It is well known that each of these factors can have a significant impact on the performance of the resultant model. Our approach employs an encoder-decoder CNN architecture, which we posit is particularly wellsuited for this task due to its ability to effectively transform data, as opposed to merely compressing it. We systematically evaluate a range of loss functions, hyperparameters, and training set sizes. Our results indicate that increasing the size of the training set has a substantial effect on reducing performance fluctuations and overall error. Additionally, we observe that the performance of the model exhibits a logarithmic dependence on the training set size. Furthermore, we investigate the effect on model performance by using different subsets of data with varying features. Our results highlight the importance of sampling the configurational space in an optimal manner, as this can have a significant impact on the performance of the model and the required training time. In conclusion, our results suggest that training a model with a pre-determined error performance bound is not a viable approach, as it does not guarantee that edge cases with errors larger than the bound do not exist. Furthermore, as most surrogate tasks involve a high dimensional landscape, an ever increasing training set size is, in principle, needed, however it is not a practical solution.

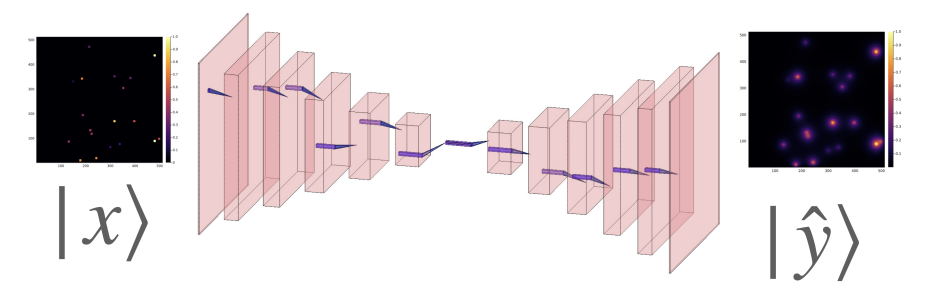
Figure 1: Sketch of the NN architecture for virtual tissue surrogate.

1,2

References

  1. Analyzing the Performance of Deep Encoder-Decoder Networks as Surrogates for a Diffusion Equation, J. Quetzalcoatl Toledo-Marin, James A. Glazier, Geoffrey Fox https://arxiv.org/pdf/2302.03786.pdf> ↩︎

  2. There is an earlier surrogate referred to in this arxiv. It was published: Toledo-Marín J. Quetzalcóatl , Fox Geoffrey , Sluka James P. , Glazier James A., Deep Learning Approaches to Surrogates for Solving the Diffusion Equation for Mechanistic Real-World Simulations,Frontiers in Physiology, Vol. 12, 2021 doi: 10.3389/fphys.2021.667828, ISSNI 1664-042X, https://www.frontiersin.org/journals/physiology/articles/10.3389/fphys.2021.667828 ↩︎

4 - Cosmoflow

The CosmoFlow training application benchmark from the MLPerf HPC v0.5 benchmark suite. It involves training a 3D convolutional neural network on N-body cosmology simulation data to predict physical parameters of the universe.

Metadata

Model cosmoflow.json

Datasets

cosmoUniverse_2019_05_4parE_tf_v2.json

cosmoUniverse_2019_05_4parE_tf_v2_mini.json

Overview

This application is based on the original CosmoFlow paper presented at SC18 and continued by the ExaLearn project, and adopted as a benchmark in the MLPerf HPC suite. It involves training a 3D convolutional neural network on N-body cosmology simulation data to predict physical parameters of the universe. The reference implementation for MLPerf HPC v0.5 CosmoFlow uses TensorFlow with the Keras API and Horovod for data-parallel distributed training. The dataset comes from simulations run by ExaLearn, with universe volumes split into cubes of size 128x128x128 with 4 redshift bins. The total dataset volume preprocessed for MLPerf HPC v0.5 in TFRecord format is 5.1 TB. The target objective in MLPerf HPC v0.5 is to train the model to a validation mean-average-error < 0.124. However, the problem size can be scaled down and the training throughput can be used as the primary objective for a small scale or shorter timescale benchmark.123

Figure 1: Example simulation of dark matter in the universe used as input to the CosmoFlow network. Copied from [NERSC](https://www.nersc.gov/news-publications/nersc-news/science-news/2018/nersc-intel-cray-harness-the-power-of-deep-learning-to-better-understand-the-universe/)

References

  1. https://proxyapps.exascaleproject.org/app/mlperf-cosmoflow/ ↩︎

  2. https://github.com/sparticlesteve/cosmoflow-benchmark ↩︎

  3. https://github.com/sparticlesteve/cosmoflow-benchmark/blob/master/README.md ↩︎

5 - Fully ionized plasma fluid model closures

The closure problem in fluid modeling is a well-known challenge to modelers aiming to accurately describe their system of interest. We will choose one of the surrogates form this application and develop a reference implementation and tutorial.

Fully ionized plasma fluid model closures (Argonne):1 The closure problem in fluid modeling is a well-known challenge to modelers aiming to accurately describe their system of interest. Analytic formulations in a wide range of regimes exist but a practical, generalized fluid closure for magnetized plasmas remains an elusive goal. There are scenarios where complex physics prevents a simple closure being assumed, and the question as to what closure to employ has a non-trivial answer. In a proof-of-concept study, Argonne researchers turned to machine learning to try to construct surrogate closure models that map the known macroscopic variables in a fluid model to the higher-order moments that must be closed. In their study, the researchers considered three closures: Braginskii, Hammett-Perkins, and Guo-Tang; for each of them, they tried three types of ANNs: locally connected, convolutional, and fully connected. Applying a physics-informed machine learning approach, they found that there is a benefit to tailoring a specific network architecture informed by the physics of the plasma regime each closure is designed for, rather than carelessly applying an unnecessarily complex general network architecture. will choose one of the surrogates and bring it up an early example for SBI with reference implementation and tutorial documentation. As a follow-up, the Argonne team will tackle more challenging problems.

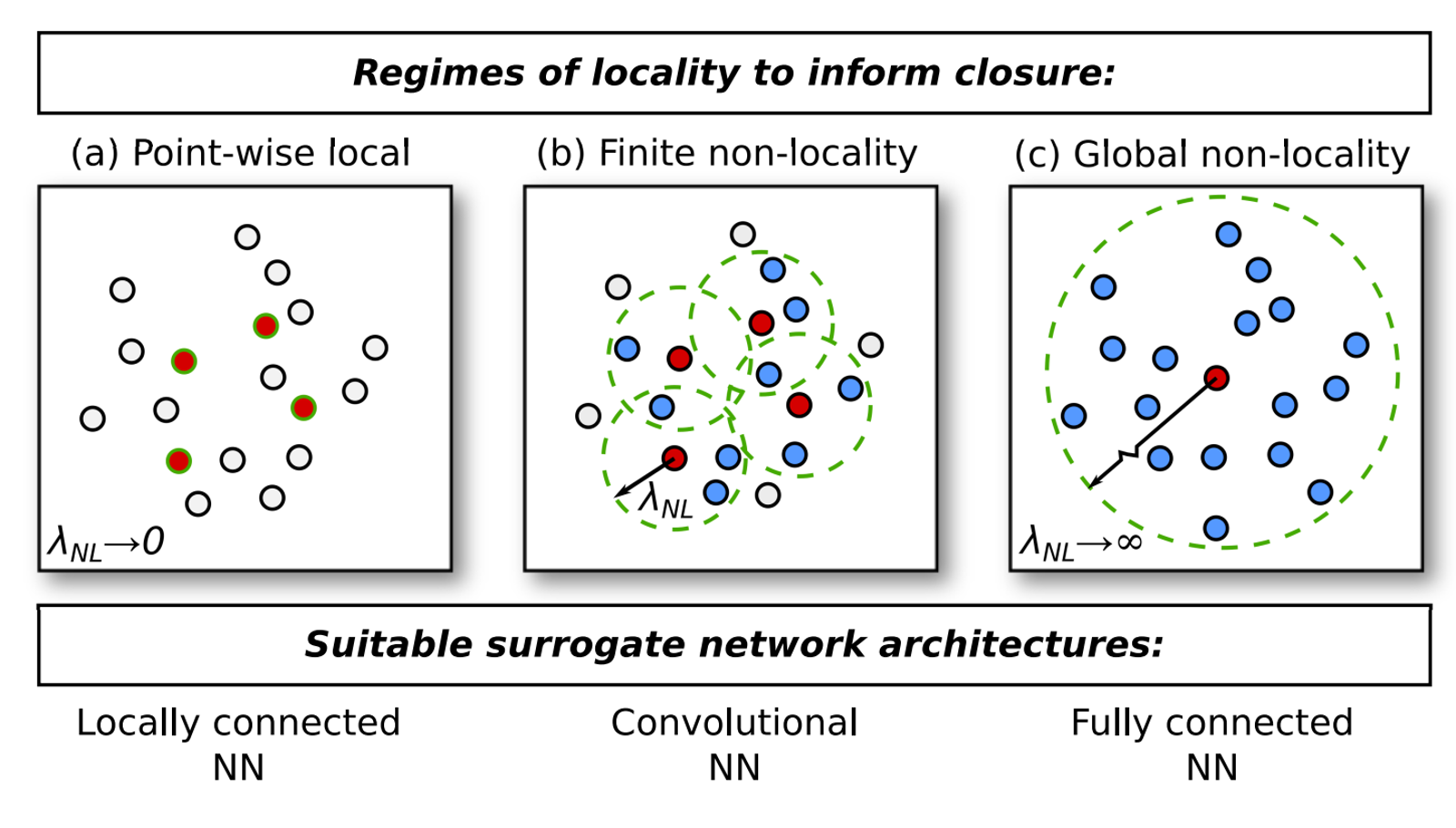
Figure 1: Simple schematic of varying classes of closure formulations.

References

  1. R. Maulik, N. A. Garland, X.-Z. Tang, and P. Balaprakash, “Neural network representability of fully ionized plasma fluid model closures,” arXiv [physics.comp-ph], 10-Feb-2020 [Online]. Available: http://arxiv.org/abs/2002.04106 ↩︎

6 - Ions in nanoconfinement

This application studies ionic structure in electrolyte solutions in nanochannels with planar uncharged surfaces and can use multiple molecular dynamics (MD) codes including LAMMPS which run on HPC supercomputers with OpenMP and MPI parallelization.

Metadata

Model nanoconfinement.json

Datasets nanoconfinement.json

This application 1 2 3 studies ionic structure in electrolyte solutions in nanochannels with planar uncharged surfaces and can use multiple molecular dynamics (MD) codes including LAMMPS 4 which run on HPC supercomputers with OpenMP and MPI parallelization.

A dense neural-net (NN) was used to learn 150 final state characteristics based on the input of 5 parameters with typical results shown in fig. 2(b) with the NN results for three important densities tracking well the MD simulation results for a wide range of unseen input system parameters. Fig. 3(a,b) shows two typical density profiles with again the NN prediction tracking well the simulation. Input quantities were confinement length, positive ion valency, negative ion valency, salt concentration, and ion diameter. Figure 2(a) shows the runtime architecture for dynamic use and update of the NN and our middleware discussed in Sec. 3.2.6 will generalize this. The inference time for this on a single core is 104 times faster than the parallel code which is itself 100 times the sequential code. This surrogate approach is the first-of-its-kind in the area of simulating charged soft-matter systems and there are many other published papers in both biomolecular and material science presenting similar successful surrogates 5 with a NN architecture similar to fig. 3(c).

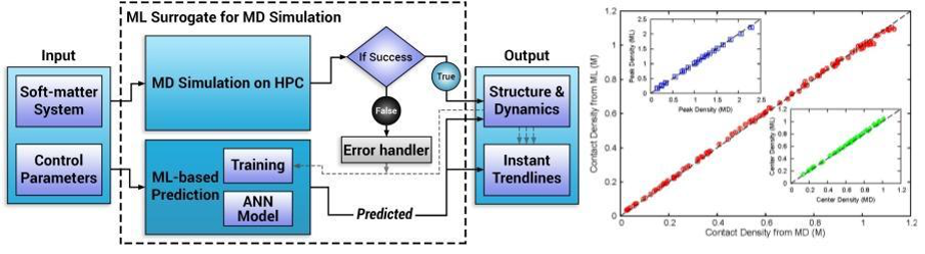
Fig. 2 a) Architecture of dynamic training of ML surrogate and b) Comparison of three final state densities (peak, contact, and center) between MD simulations and NN surrogate predictions [^5] [^51].

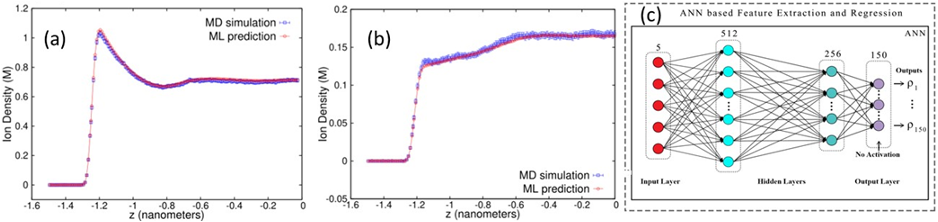
Fig. 3 (a,b) Two density profiles of confined ions for very different input parameters and comparing MD and NN. (c) Fully connected deep learning network used to learn the final densities. ReLU activation units are in the 512 and 256 node hidden layers. The output values were learned on 150 nodes.

References

  1. JCS Kadupitiya , Geoffrey C. Fox , and Vikram Jadhao, “Machine learning for performance enhancement of molecular dynamics simulations,” in International Conference on Computational Science ICCS2019, Faro, Algarve, Portugal, 2019 [Online]. Available: http://dsc.soic.indiana.edu/publications/ICCS8.pdf ↩︎

  2. J. C. S. Kadupitiya, F. Sun, G. Fox, and V. Jadhao, “Machine learning surrogates for molecular dynamics simulations of soft materials,” J. Comput. Sci., vol. 42, p. 101107, Apr. 2020 [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1877750319310609 ↩︎

  3. “Molecular Dynamics for Nanoconfinement.” [Online]. Available: https://github.com/softmaterialslab/nanoconfinement-md. [Accessed: 11-May-2020] ↩︎

  4. S. Plimpton, “Fast Parallel Algorithms for Short Range Molecular Dynamics,” J. Comput. Phys., vol. 117, pp. 1–19, 1995 [Online]. Available: http://faculty.chas.uni.edu/~rothm/Modeling/Parallel/Plimpton.pdf ↩︎

  5. Geoffrey Fox, Shantenu Jha, “Learning Everywhere: A Taxonomy for the Integration of Machine Learning and Simulations,” in IEEE eScience 2019 Conference, San Diego, California [Online]. Available: https://arxiv.org/abs/1909.13340 ↩︎

7 - miniWeatherML

A simplified weather model simulating flows such as supercells that are realistic enough to be challenging and simple enough for rapid prototyping in creating and learning about surrogates.

Metadata

Model miniWeatherML.json

Datasets miniWeatherML.json

Overview

MiniWeatherML is a playground for learning and developing Machine Learning (ML) surrogate models and workflows. It is based on a simplified weather model simulating flows such as supercells that are realistic enough to be challenging and simple enough for rapid prototyping in:

  • Data generation and curation
  • Machine Learning model training
  • ML model deployment and analysis
  • End-to-end workflows

Figure 1: CANcer Distributed Learning Environment

1,2

References

  1. https://github.com/mrnorman/miniWeatherML, ↩︎

  2. https://github.com/mrnorman/miniWeatherML/wiki ↩︎

8 - OSMI

We explore the relationship between certain network configurations and the performance of distributed Machine Learning systems. We build upon the Open Surrogate Model Inference (OSMI) Benchmark, a distributed inference benchmark for analyzing the performance of machine-learned surrogate models

Overview

We explore the relationship between certain network configurations and the performance of distributed Machine Learning systems. We build upon the Open Surrogate Model Inference (OSMI) Benchmark, a distributed inference benchmark for analyzing the performance of machine-learned surrogate models developed by Wes Brewer et. Al. We focus on analyzing distributed machine-learning systems, via machine-learned surrogate models, across varied hardware environments. By deploying the OSMI Benchmark on platforms like Rivanna HPC, WSL, and Ubuntu, we offer a comprehensive study of system performance under different configurations. The paper presents insights into optimizing distributed machine learning systems, enhancing their scalability and efficiency. We also develope a framework for automating the OSMI benchmark.

Introdcution

With the proliferation of machine learning as a tool for science, the need for efficient and scalable systems is paramount. This paper explores the Open Surrogate Model Inference (OSMI) Benchmark, a tool for testing the performance of machine-learning systems via machine-learned surrogate models. The OSMI Benchmark, originally created by Wes Brewer and colleagues, serves to evaluate various configurations and their impact on system performance.

Our research pivots around the deployment and analysis of the OSMI Benchmark across various hardware platforms, including the high-performance computing (HPC) system Rivanna, Windows Subsystem for Linux (WSL), and Ubuntu environments.

In each experiment, there are a variable number of TensorFlow model server instances, overseen by a HAProxy load balancer that distributes inference requests among the servers. Each server instance operates on a dedicated GPU, choosing between the V100 or A100 GPUs available on Rivanna. This setup mirrors real-world scenarios where load balancing is crucial for system efficiency.

On the client side, we initiate a variable number of concurrent clients executing the OSMI benchmark to simulate different levels of system load and analyze the corresponding inference throughput.

On top of the original OSMI-Bench, we implemented an object-oriented interface in Python for running experiments with ease, streamlining the process of benchmarking and analysis. The experiments rely on custom-built images based on NVIDIA’s tensorflow image. The code works on several hardwares, assuming the proper images are built.

Additionally, We develop a script for launching simultaneous experiments with permutations of pre-defined parameters with Cloudmesh Experiment-Executor. The Experiment Executor is a tool that automates the generation and execution of experiment variations with different parameters. This automation is crucial for conducting tests across a spectrum of scenarios.

Finally, we analyze the inference throughput and total time for each experiment. By graphing and examining these results, we draw critical insights into the performance dynamics of distributed machine learning systems.

In summary, a comprehensive examination of the OSMI Benchmark in diverse distributed ML systems is provided. We aim to contribute to the optimization of these systems, by providing a framework for finding the best performant system configuration for a given use case. Our findings pave the way for more efficient and scalable distributed computing environments.

The architectural view of the benchmarks are depictued in Figure 1 and Figure 2.

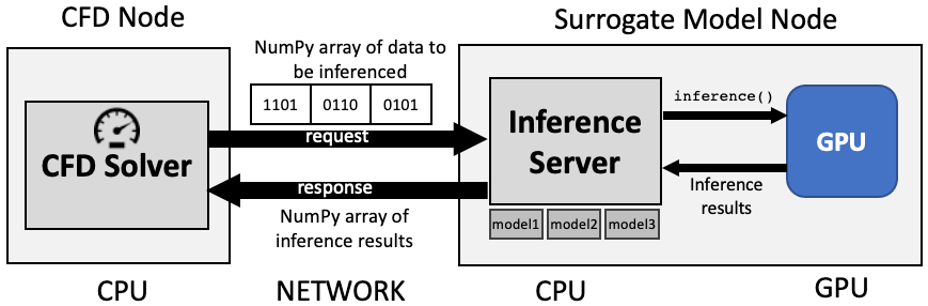
Figure 1: Surrogate calculations via a Inference Server.

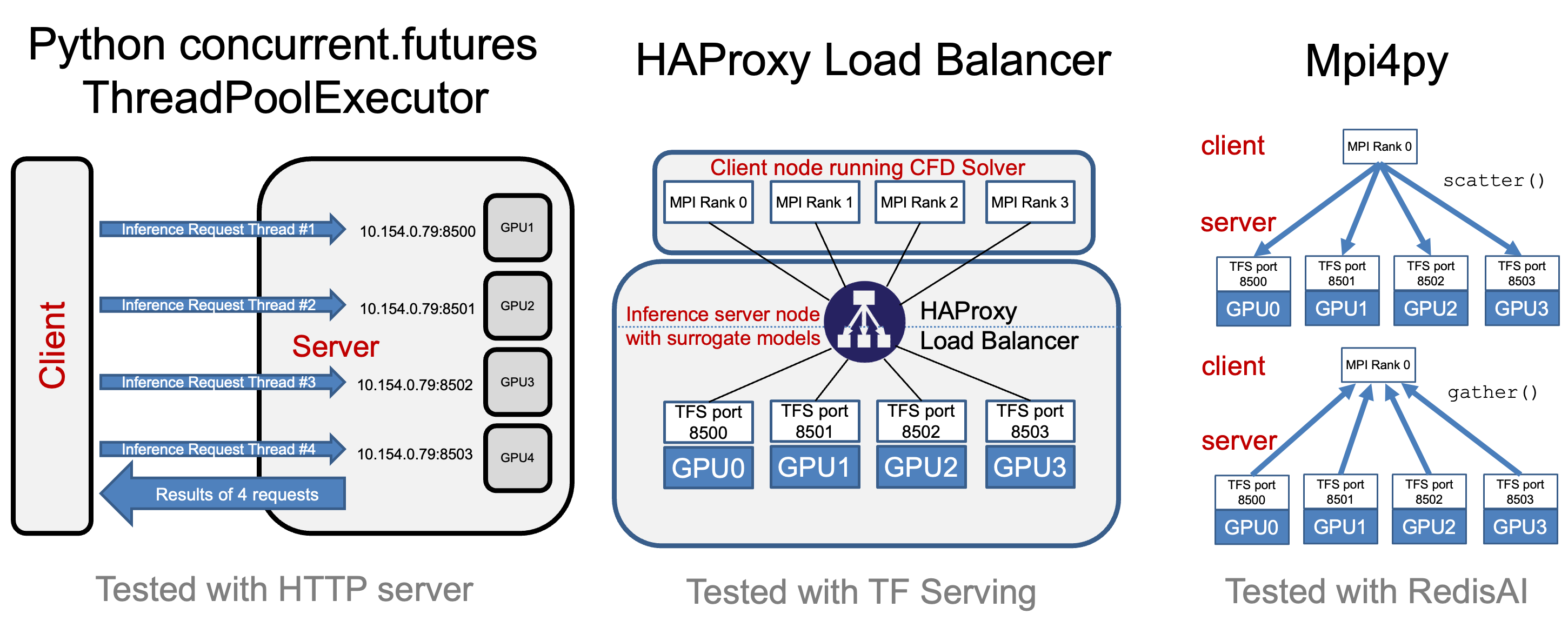
Figure 2: Possible benchmark configurations to measure sped of parallel iference.

12345

References

  1. Brewer, Wesley, Daniel Martinez, Mathew Boyer, Dylan Jude, Andy Wissink, Ben Parsons, Junqi Yin, and Valentine Anantharaj. “Production Deployment of Machine-Learned Rotorcraft Surrogate Models on HPC.” In 2021 IEEE/ACM Workshop on Machine Learning in High Performance Computing Environments (MLHPC), pp. 21-32. IEEE, 2021, https://ieeexplore.ieee.org/abstract/document/9652868, Note that OSMI-Bench differs from SMI-Bench described in the paper only in that the models that are used in OSMI are trained on synthetic data, whereas the models in SMI were trained using data from proprietary CFD simulations. Also, the OSMI medium and large models are very similar architectures as the SMI medium and large models, but not identical. ↩︎

  2. Brewer, Wesley, Greg Behm, Alan Scheinine, Ben Parsons, Wesley Emeneker, and Robert P. Trevino. “iBench: a distributed inference simulation and benchmark suite.” In 2020 IEEE High Performance Extreme Computing Conference (HPEC), pp. 1-6. IEEE, 2020. ↩︎

  3. Brewer, Wesley, Greg Behm, Alan Scheinine, Ben Parsons, Wesley Emeneker, and Robert P. Trevino. “Inference benchmarking on HPC systems.” In 2020 IEEE High Performance Extreme Computing Conference (HPEC), pp. 1-9. IEEE, 2020. ↩︎

  4. Brewer, Wesley, Chris Geyer, Dardo Kleiner, and Connor Horne. “Streaming Detection and Classification Performance of a POWER9 Edge Supercomputer.” In 2021 IEEE High Performance Extreme Computing Conference (HPEC), pp. 1-7. IEEE, 2021. ↩︎

  5. Gregor von Laszewski, J. P. Fleischer, and Geoffrey C. Fox. 2022. Hybrid Reusable Computational Analytics Workflow Management with Cloudmesh. https://doi.org/10.48550/ARXIV.2210.16941 ↩︎

9 - Particle dynamics

Recurrent Neural Nets as a Particle Dynamics Integrator

Recurrent Neural Nets as a Particle Dynamics Integrator

The second IU initial application shows a rather different type of surrogate and illustrates an SBI goal to collect benchmarks covering a range of surrogate designs. Molecular dynamics simulations rely on numerical integrators such as Verlet to solve Newton’s equations of motion. Using a sufficiently small time step to avoid discretization errors, Verlet integrators generate a trajectory of particle positions as solutions to the equations of motions. In 1, 2, 3, the IU team introduces an integrator based on recurrent neural networks that is trained on trajectories generated using the Verlet integrator and learns to propagate the dynamics of particles with timestep up to 4000 times larger compared to the Verlet timestep. As shown in Fig. 4 (right) the error does not increase as one evolves the system for the surrogate while standard Verlet integration in Fig. 4 (left) has unacceptable errors even for time steps of just 10 times that used in an accurate simulation. The surrogate demonstrates a significant net speedup over Verlet of up to 32000 for few-particle (1 - 16) 3D systems and over a variety of force fields including the Lennard-Jones (LJ) potential. This application uses a recurrent plus dense neural network architecture and illustrates an important approach to learning evolution operators which can be applied across a variety of fields including Earthquake science (IU work in progress) and Fusion 4.

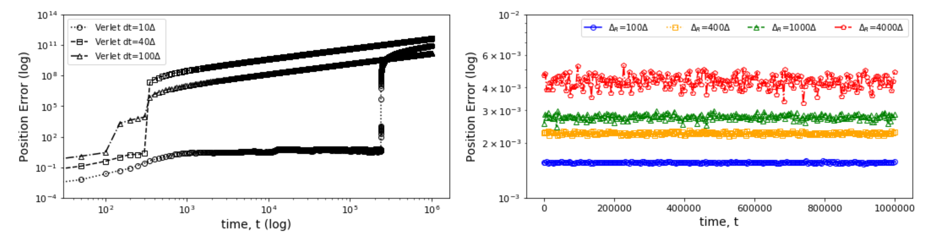
Fig. 4: Average error in position updates for 16 particles interacting with an LJ potential, The left figure is standard MD with error increasing for ∆t as 10, 40, or 100 times robust choice (0.001). On the right is the LSTM network with modest error up to t = 106 even for ∆t = 4000 times the robust MD choice.

References

  1. JCS Kadupitiya, Geoffrey C. Fox, Vikram Jadhao, “GitHub repository for Simulating Molecular Dynamics with Large Timesteps using Recurrent Neural Networks.” [Online]. Available: https://github.com/softmaterialslab/RNN-MD. [Accessed: 01-May-2020] ↩︎

  2. J. C. S. Kadupitiya, G. C. Fox, and V. Jadhao, “Simulating Molecular Dynamics with Large Timesteps using Recurrent Neural Networks,” arXiv [physics.comp-ph], 12-Apr-2020 [Online]. Available: http://arxiv.org/abs/2004.06493 ↩︎

  3. J. C. S. Kadupitiya, G. Fox, and V. Jadhao, “Recurrent Neural Networks Based Integrators for Molecular Dynamics Simulations,” in APS March Meeting 2020, 2020 [Online]. Available: http://meetings.aps.org/Meeting/MAR20/Session/L45.2. [Accessed: 23-Feb-2020] ↩︎

  4. J. Kates-Harbeck, A. Svyatkovskiy, and W. Tang, “Predicting disruptive instabilities in controlled fusion plasmas through deep learning,” Nature, vol. 568, no. 7753, pp. 526–531, Apr. 2019 [Online]. Available: https://doi.org/10.1038/s41586-019-1116-4 ↩︎

10 - PtychoNN: deep learning network for ptychographic imaging that predicts sample amplitude and phase from diffraction data.

A DL-based approach to solve the ptychography data inversion problem that learns a direct mapping from the reciprocal space data to the sample amplitude and phase.

Metadata

Model ptychonn.json

Datasets ptychonn_20191008_39.json

PtychoNN, uses a deep convolutional neural network to predict realspace structure and phase from far-field diffraction data. It recovers high fidelity amplitude and phase contrast images of a real sample hundreds of times faster than current ptychography reconstruction packages and reduces sampling requirements 1

References

  1. Mathew J. Cherukara, Tao Zhou, Youssef Nashed, Pablo Enfedaque, Alex Hexemer, Ross J. Harder, Martin V. Holt; AI-enabled high-resolution scanning coherent diffraction imaging. Appl. Phys. Lett. 27 July 2020; 117 (4): 044103. https://doi.org/10.1063/5.0013065 ↩︎